Application One: Diffraction

Problem Introduction

• what is diffraction: inteference patterns that light makes passing through apertures

• how to make:

  • light from a distant source, which means the aperture plain is a wavefront i.e. wave have the same phase at all points of the aperture

  • plain with apertures

  • image plain at some distance

• assumptions:

  • light is an oscollating E/M field

  • light is monochromatic (only one frequency)

  • light of the aperture plain as:

  \[E_0 \cdot e^{2 \pi i \nu t}\]

where \(E_0\) is strength of the field on the aperture plain and \(\nu\) is frequency (monochromatic)

Near-Field vs. Far-Field

Distance between the aperture plain and the image plain (measured relative to the wavelength) determines diffraction

• near-field Fresnel diffraction

• far-field Fraunhofer diffraction

Huygens Principle

Each point on a wavefront can be regarded as a source i.e. all the sources on the wavefront will be integrated

Question: what is the strength of the wave on point \(P\)?

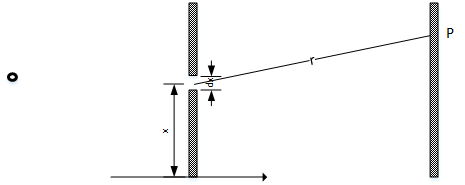
Solutioin

After introducing coordinates on the aperture plain, it is clear that the main effect in light going from \(X\) to \(P\) over a certain distance is: change in phase. The distance \(r\) can be represented as \(\frac{r}{\lambda}\) cycles, which means a phase change of \(\frac{2 \pi r}{\lambda}\). Therefore the light magnitude of \(P\) resulted from a tiny source of point \(x\) of the aperture plain is:

\[dE = E_0 \cdot e^{2 \pi i \nu t} \cdot e^{-2 \pi i \frac{r}{\lambda}} dx\]

therefore the total field is the integral over the aperture:

\[\begin{split}E_{P} & = \int E_0 \cdot e^{2 \pi i \nu t} \cdot e^{-2 \pi i \frac{r}{\lambda}} dx \\ & = E_{0} \cdot e^{2 \pi i \nu t} \int e^{-2 \pi i \frac{r}{\lambda}} dx \\ & = E_{0} \cdot e^{2 \pi i \nu t} \int_{-\infty}^{+\infty} e^{-2 \pi i \frac{r}{\lambda}} A(x) dx\end{split}\]

where \(r\) (not \(t\)) depends on \(x\) and \(A(x)\) is the aperture function:

\[\begin{split}A(x) = \begin{cases} 1 & x \in \text{aperture} \\ 0 & \text{otherwise} \end{cases}\end{split}\]

with Fraunhofer approximation:

\[r = r_0 - x sin \theta\]

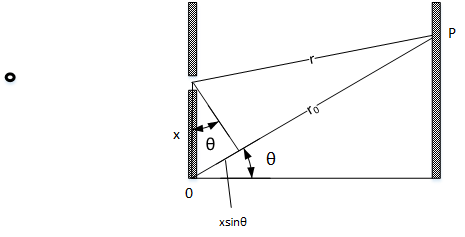
The integral can be re-written as:

\[\begin{split}\int_{-\infty}^{+\infty} e^{-2 \pi i \frac{r}{\lambda}} A(x) dx & = \int_{-\infty}^{\infty} e^{2 \pi i \frac{x sin \theta - r_0}{\lambda}} A(x) dx \\ & = e^{-2 \pi i \frac{r_0}{\lambda}} \int_{-\infty}^{+\infty} e^{2 \pi i x p} A(x) dx\end{split}\]

where axillary variable \(p\):

\[p = \frac{sin \theta}{\lambda}\]

\[\begin{split}\therefore E_P & = C \int_{-\infty}^{+\infty} e^{2 \pi i x p} A(x) dx \\ & = C \cdot \mathcal{F}^{-1} A (p)\end{split}\]

\[\tag*{$\blacksquare$}\]

Conclusion: for far-field diffraction, the intensity of the light is the magnitude of the inverse Fourier transform of the aperture function.

Back to Fourier Transform.